Matematik-IT bygger på enkla principer, som även unga elever kan lära sig använda och med hjälp av datorns beräkningskraft utforska världen i all sin komplexitet. Denna post ger i några korta datorprogram en inledning till den spännande värld av Matematik-IT, som sedan utforskas i mer detalj i en serie poster av vilka många är representerade på App Store. Se huvudmenyn Spel 1-100.
Huvudmenyn beskriver olika aspekter av Matematik-IT.
1. Konstruktion av de Naturliga Talen.
Matematikern Leopold Kronecker (1823-1891) sade: Gud gav oss de naturliga talen 1,2,3,…, resten är människans skapelse. Låt oss här istället själva med hjälp av spelplattformen Codea konstruera de naturliga talen genom att upprepning av +1, och skriva ut dem på konsol och skärm.
–Konstruktion av naturliga tal
function setup()
print(“Konstruera de Naturliga Talen 1,2,3,…”)
print(“Skriv på Konsolen och Skärmen”)
n=0
end
function draw()
background(40, 40, 50)
n=n+1
print(n)
font(“AmericanTypewriter”)
fontSize(50)
text(n,300,500)
end
2. Utforska Skärmens Pixlar
function setup()
print(“Utforska Skärmens Pixlar”)
end
function draw()
background(40, 40, 50)
font(“AmericanTypewriter”)
fontSize(50)
fill(238, 16, 46, 255)
text(CurrentTouch.x,CurrentTouch.x,CurrentTouch.y)
text(CurrentTouch.y,CurrentTouch.x,CurrentTouch.y-50)
end
3. Konstruktion av Binära Heltal
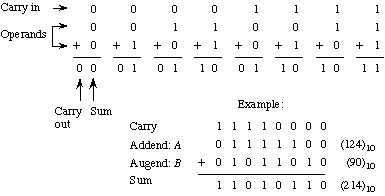
Binära tal använder de två siffrorna 1 och 0, med följande räkneregler: 0+0=0, 1+0=1, 0+1=1, 1+1 =10, där således med vanliga siffror 10 (binärt) = 2 (decimalt), 100 (binärt) = 4 (decimalt), 111 (binärt) = 7 (decimalt) osv.
Med binära tal kan barn lära sig addera, subtrahera och multiplicera godtyckliga heltal från 4 år. Datorn räknar också binärt, eftersom det är enkelt och går fort.
function setup()
print(“Binär Representation av Naturliga Tal via Tabell/Lista”)
bit={}
I=100
for i=1,I do
bit[i]=0
end
end
function draw()
background(40, 40, 50)
bit[1]=bit[1]+1
for i=1,I do
if bit[i]>1 then
bit[i+1]=bit[i+1]+1
bit[i]=0
end
end
font(“AmericanTypewriter”)
fontSize(50)
fill(238, 16, 46, 255)
for i=1,I do
text(bit[i],700-50*i,800)
end
end
4. Lutning av Skärmen: Ratt
Styrning av vår färd genom världen är fundamental för överlevnad och glädje. En iPad ger möjlighet till styrning via lutning av plattan i form av ratt-styrning som i en bil eller gravitationskraft-styrning som genom lutande plan.
function setup()
print(“Lutning som Ratt”)
pos=vec2(0,0)
end
function draw()
sprite(“SpaceCute:Background”,WIDTH/2,HEIGHT/2,HEIGHT)
pos=pos+20*vec2(Gravity.x,Gravity.y)
sprite(“SpaceCute:Beetle Ship”,pos.x,pos.y,100)
end
5. Lutning av Skärmen: Kraft
Jämför rattstyrning med kraftstyrning och upplev att det kraftstyrning är mycket svårare.
function setup()
print(“Lutning som Ratt”)
pos=vec2(0,0)
vel=vec2(0,0)
dt=0.1
end
function draw()
sprite(“SpaceCute:Background”,WIDTH/2,HEIGHT/2,HEIGHT)
vel=vel+20*vec2(Gravity.x,Gravity.y)*dt
pos=pos+vel*dt
sprite(“SpaceCute:Beetle Ship”,pos.x,pos.y,100)
end
6. Newtons mekanik: Basic
function setup()
print(“Newtons ekvationer”)
pos={}
hast={}
acc={}
N=10
for n=1,N do
pos[n]=vec2(math.random(-100,100),math.random(-100,100))
hast[n]=math.random(-2,2)*vec2(pos[n].y,-pos[n].x)
acc[n]=vec2(0,0)
end
dt=0.1
end
function draw()
background(40, 40, 50)
fontSize(50)
fill(219, 14, 36, 255)
text(“Newtons ekvationer:”,300,900)
text(“a=F/m, dv=adt, dx=vdt”,300,800)
for n=1,N do
acc[n]=-pos[n]
hast[n]=hast[n]+acc[n]*dt
pos[n]=pos[n]+hast[n]*dt
sprite(“SpaceCute:Star”,pos[n].x+300,pos[n].y+500,100)
end
end
7. Newtons Mekanik: Planetsystem
function setup()
I=20
print(“Planet”)
print(“force~1/r^2”)
print(“acc=force/mass”)
print(“vel=vel+acc*dt”)
print(“pos=pos+vel*dt”)
pos = {}
vel = {}
acc= {}
force = {}
m={}
dt =0.001
for i=1,I do
pos[i]=vec2(math.random(200,400),math.random(300,600))
vel[i]=vec2(math.random(-100,100),math.random(-100,100))
m[i] = math.random(1,100)
end
end
function draw()
font(“AmericanTypewriter-Condensed”)
fontSize(30)
fill(0, 22, 255, 255)
text(“Motion-Force: Newton’s 2nd Law”,250, 800)
text(“force = mass x acceleration, f = m x a”,250, 750)
text(“acc=force/mass”,250, 700)
text(“vel=vel+acc*dt”,250, 650)
text(“pos=pos+vel*dt”,250, 600)
stroke(43, 203, 22, 108)
strokeWidth(1)
for i=1,I do
force[i]=vec2(0,0)
for j=1,I do
r = (pos[i]-pos[j]):len()
force[i]=force[i]-(1000000/(r+10)^3)*(pos[i]-pos[j])
end
acc[i] = force[i]
vel[i]=vel[i]+acc[i]*dt
pos[i]=pos[i]+vel[i]*dt
end
fill(42, 0, 255, 255)
for i=1,I do
ellipse(pos[i].x,pos[i].y,10,10)
end
end
8. Parametrar
function setup()
print(“Parameter”)
parameter.integer(“Radie”,1,200,10)
parameter.number(“Massa”,0,1,0.5)
end
function draw()
background(40, 40, 50)
sprite(“SpaceCute:Health Heart”,300,500,Radie)
text(Massa,300,300)
end
9. Touch
function setup()
print(“Touch Me!”)
started=vec2(0,0)
moving=vec2(0,0)
finished=vec2(0,0)
end
function draw()
background(40, 40, 50)
fontSize(30)
fill(7, 7, 232, 255)
text(started.x,started.x,started.y)
text(started.y,started.x,started.y-50)
fill(5, 255, 0, 255)
text(moving.x,moving.x+100,moving.y)
text(moving.y,moving.x+100,moving.y-50)
fill(255, 0, 10, 255)
text(finished.x,finished.x,finished.y)
text(finished.y,finished.x,finished.y-50)
end
function touched(touch)
if CurrentTouch.state==BEGAN then
started=vec2(CurrentTouch.x,CurrentTouch.y)
end
if CurrentTouch.state==MOVING then
moving=vec2(CurrentTouch.x,CurrentTouch.y)
end
if CurrentTouch.state==ENDED then
finished=vec2(CurrentTouch.x,CurrentTouch.y)
end
end
10. Knappar
function setup()
print(“Knapp”)
knapp=vec2(300,500)
switch=1
end
function draw()
background(40, 40, 50)
if switch==1 then
sprite(“Space Art:UFO”,300,500,100)
fontSize(50)
fill(255, 0, 3, 255)
text(“On”,300,600)
end
if switch==-1 then
sprite(“Space Art:UFO”,300,500,50)
fontSize(50)
fill(0, 255, 62, 255)
text(“Off”,300,600)
end
end
function touched(touch)
dist=(vec2(CurrentTouch.x,CurrentTouch.y)-knapp):len()
if CurrentTouch.state==ENDED and dist < 20 then
switch=-switch
end
end
11. Pong
pos =vec2(WIDTH/2,HEIGHT/2)
vel =vec2(100,100)
acc =vec2(0,0)
dt = 0.1
displayMode(FULLSCREEN)
function setup()
print(“Pong”)
music(“Game Music One:Venus”,true,0.5)
end
function draw()
background(26, 231, 38, 255)
if pos.x>WIDTH then
vel.x=-vel.x
end
if pos.x1000 then
vel.y=-vel.y
end
fill(0, 56, 255, 255)
rect(CurrentTouch.x-100,100,200,40)
if (pos.x>CurrentTouch.x-100 and pos.x<CurrentTouch.x+100) and (pos.y<50) then
vel.y=-vel.y
end
vel = vel +acc*dt
pos = pos +vel*dt
fill(255, 24, 0, 255)
ellipse(pos.x,pos.y,40)
end
12. Många Bollar
function setup()
print(“Många studsande bollar som interagerar genom elastiska fjädrar som aktiveras då bollarna är i kontakt.”)
print(“Bollars position kan ändras via touch.”)
print(“Styrning av bollradie R, fjäderstyvhet E, dämpning D och gravitation D.”)
speech.volume=1
speech.rate=0.01
speech.say(“Many bouncing balls having a ball”)
I=20
parameter.number(“R”,1,200,50)
parameter.number(“E”,10,1000,100)
parameter.number(“G”,-1000,1000,100)
parameter.number(“D”,0,100,10)
x={}
xold={}
xm={}
v={}
vold={}
vm={}
a={}
f={}
F={}
mass={}
for i=1,I do
x[i]=vec2(math.random(100,400),math.random(100,800))
xold[i]=vec2(math.random(100,400),math.random(100,800))
xm[i]=vec2(math.random(100,400),math.random(100,800))
v[i]=vec2(0,0)
vold[i]=vec2(0,0)
vm[i]=vec2(0,0)
f[i]=vec2(0,0)
a[i]=vec2(0,0)
mass[i]=1
end
dt=0.01
n=0
t=0
end
function draw()
t=t+dt
print(t)
background(40, 40, 50)
fill(0, 68, 255, 255)
rect(0,200,1000,20)
rect(10,200,20,1000)
rect(450,200,20,1000)
for i=1,I do
fill(255, 0, 40, 255)
ellipse(x[i].x,x[i].y,R)
end
for p=1,4 do
for i=1,I do
f[i]=vec2(0,-G)
for j=1,I do
xm[i]=(x[i]+xold[i])/2
vm[i]=(v[i]+vold[i])/2
length=(xm[i]-xm[j]):len()
if length f[i]=f[i]+E*(xm[i]-xm[j])
end
end
if x[i].y f[i].y=f[i].y+E*10*(250-x[i].y)
end
if x[i].x420 then
f[i].x=f[i].x+E*10*(420-x[i].x)
end
a[i]=f[i]/mass[i]
v[i]=(1-0.001*D)*vold[i]+a[i]*dt
x[i]=xold[i]+vm[i]*dt
end
end
for i=1,I do
xold[i]=x[i]
vold[i]=v[i]
end
end
function touched(touch)
if touch.state==ENDED then
n=n+1
x[n]=vec2(CurrentTouch.x,CurrentTouch.y)
xm[n]= x[n]
xold[n]= x[n]
fill(255, 0, 40, 255)
ellipse(x[n].x,x[n].y,R)
end
end
12. Massor och Fjädrar
function setup()
print(“Kedja av Massor och Fjädrar”)
print(“Touch för att skapa massor länkade med fjädrar”)
links = {}
linkvels = {}
dt = 0.01
force = vec2(0,0)
N=0
end
function draw()
background(40, 40, 50)
for k,link in pairs(links) do
fill(255, 0, 54, 255)
strokeWidth(0)
ellipse(links[k].x,links[k].y,40)
if k>1 then
stroke(0, 255, 66, 255)
strokeWidth(10)
line(links[k].x,links[k].y,links[k-1].x,links[k-1].y)
end
if k>2 then
for m=1,4 do
force = (links[k-2] – 2*links[k-1]+links[k])
linkvels[k-1]=linkvels[k-1]+force*dt
links[k-1]=links[k-1]+linkvels[k-1]*dt
end
end
if k force =vec2(0,0)
linkvels[1]=linkvels[1]+force*dt
links[1]=links[1]+linkvels[1]*dt
end
end
end
function touched(touch)
if touch.state == BEGAN then
N=N+1
table.insert(links, makeLink(touch.x,touch.y))
table.insert(linkvels, makeLinkVel())
end
if touch.state == ENDED then
links[N].x = touch.x
links[N].y = touch.y
end
end
function makeLink(x,y)
local link=vec2()
link.x = x
link.y = y
return link
end
function makeLinkVel()
local linkvel=vec2(0,0)
return linkvel
end
13. Fysikmotor
function setup()
print(“Test av fysikmotorn”)
N=100
body={}
for n=1,N do
body[n]=physics.body(CIRCLE,10)
body[n].x=math.random(150,600)
body[n].y=math.random(150,1000)
body[n].linearVelocity=vec2(math.random(-100,100),math.random(-100,100))
body[n].restitution=1
end
floor=physics.body(POLYGON,vec2(0,0),vec2(1000,0),vec2(1000,50),vec2(0,50))
floor.x=100
floor.y=100
floor.r=0
floor.type=STATIC
wall1=physics.body(POLYGON,vec2(0,0),vec2(20,0),vec2(20,1000),vec2(0,1000))
wall1.x=100
wall1.y=100
wall1.r=0
wall1.type=STATIC
wall2=physics.body(POLYGON,vec2(0,0),vec2(20,0),vec2(20,1000),vec2(0,1000))
wall2.x=700
wall2.y=100
wall2.r=0
wall2.type=STATIC
physics.gravity(0,-10)
end
function draw()
background(246, 246, 247, 255)
for n=1,N do
sprite(“SpaceCute:Beetle Ship”,body[n].x,body[n].y,20)
end
fill(0, 26, 255, 255)
rect(floor.x-200,floor.y+25,1000,20)
rect(wall1.x,wall1.y,20,1000)
rect(wall2.x,wall1.y,20,1000)
end
14. Hoppande Apa
Vi tränar på fysikmotorn enligt post 52.
15. Input av Text från Skärmen
Se post 51.
16. Interaktiv Berättelse
Vi tittar på hur man kan skapa en interaktiv animerad berättelse utifrån post 50.
.
.
,
or
.


 One can use a standard 10 bead Abacus with N rows for binary computation, for example as follows:
One can use a standard 10 bead Abacus with N rows for binary computation, for example as follows: